Branch-Line Coupler

Introduction

This is a microstrip Branch-Line coupler designed over a 20 mil RO4003C.

The Branch-Line coupler is one of the easiest couplers to design, and it is very common and well known in the literature. It consists of four λ/4 transmission lines: the series lines are Z₀/√2 Ω and the shunt lines are Z₀ Ω.

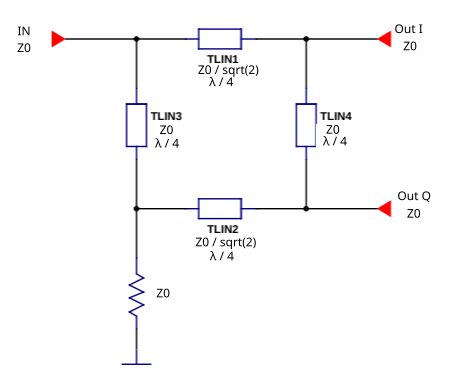
Features

Simple design
Easy to fabricate in microstrip
Good port isolation
Equal power split (3 dB)
90° phase difference between output ports
All ports are matched simultaneously

Warning

Narrow bandwidth (~10–20%)
Large size at low frequencies

References

David M. Pozar, Microwave Engineering, 4th Edition, 2012. Chapter 7.5
Unknown Editor, Microwaves101, Branchline Couplers

Specifications

Feature	Value
Band	[1800, 2200] MHz
Insertion Loss (I/Q)	3.5 ± 0.5 dB
I/Q phase difference	90±2 deg
Return Loss	<-12 dB
I/Q Isolation	>12 dB

Design Procedure

1. Ideal Transmission Line Implementation

As a first approach, the Branch-Line is designed with ideal transmission lines to see its behavior. This can be done in Qucs-S using the Qucsator-RF backend.

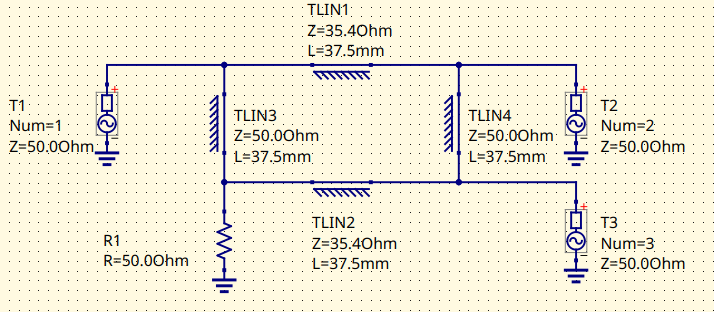
../../../_images/1_TLIN_Schematic.png — Branch-Line schematic with ideal transmission lines

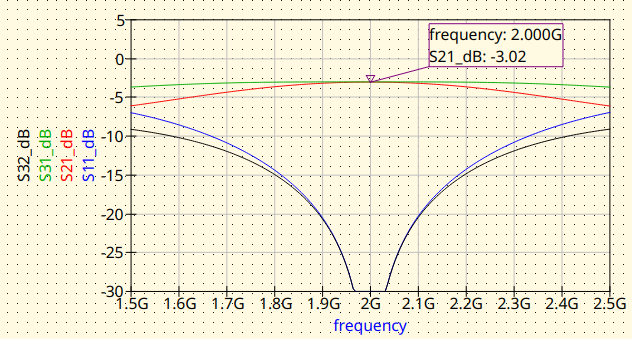
../../../_images/1_TLIN_Magnitude.png — Branch-Line with ideal transmission lines. Magnitude response

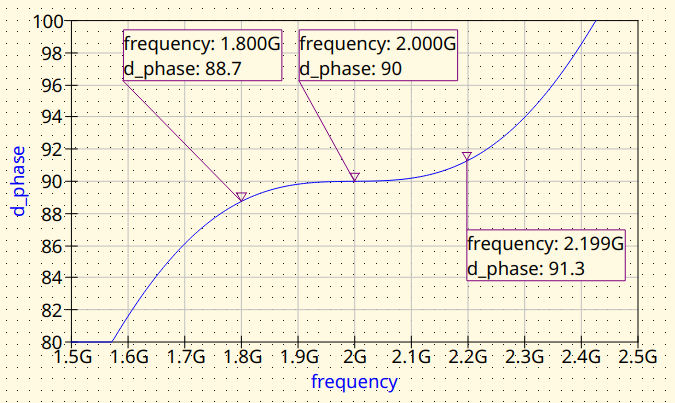
../../../_images/1_TLIN_DPhase.png — Branch-Line with ideal transmission lines. Phase difference between outputs

2. Microstrip (MS) Line Implementation

The ideal transmission lines are replaced by microstrip transmission lines. The synthesis can be done with the Transmission Line tool from Qucs-S or directly with the RF Circuit Synthesis Tools embedded in the Qucs-S S-Parameter Viewer, both tools are included in the Qucs-S suite.

2.1 MS: No Junctions nor Feed Lines

The ideal transmission lines by microstrip lines. The junctions and the feed lines are not included at this stage. This approach will let to evaluate the impact of the junctions and also, the feedlines later.

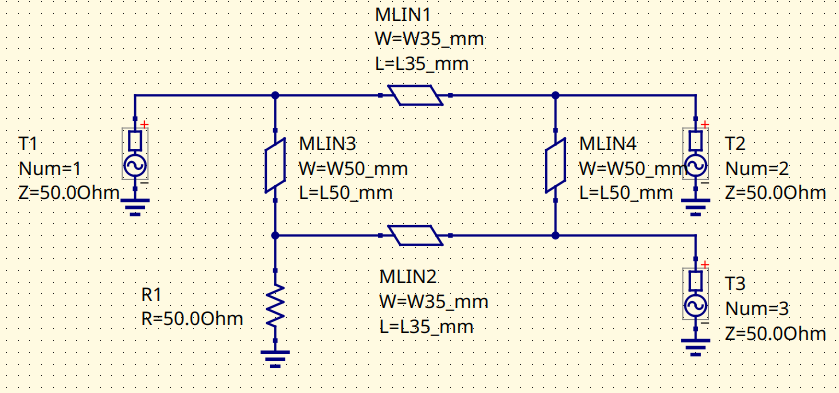
../../../_images/2_1_MLIN_No_Junctions_Schematic.png — Branch-Line with microstrip lines. Schematic

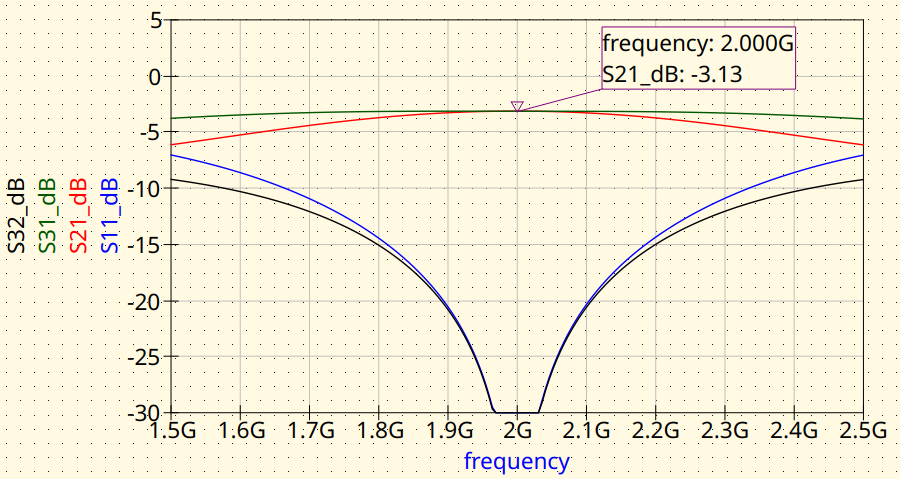
../../../_images/2_1_MLIN_No_Junctions_Magnitude.png — Branch-Line with microstrip lines. Magnitude response

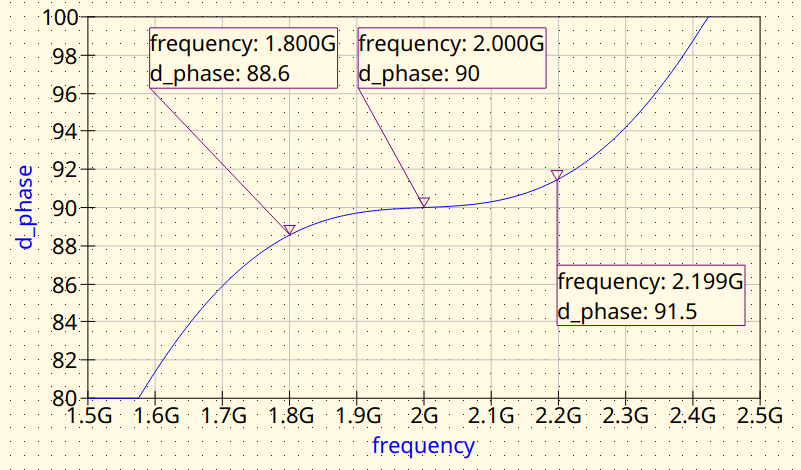
../../../_images/2_1_MLIN_No_Junctions_DPhase.png — Branch-Line with microstrip lines. Phase difference between outputs

2.2 MS: Add Junctions and Feed Lines

The tee junctions and the feed lines are added. Notice that the tee junctions pull the center frequency down. The feed lines have no effect on the response as they are 50 Ω lines, they only add some insertion loss.

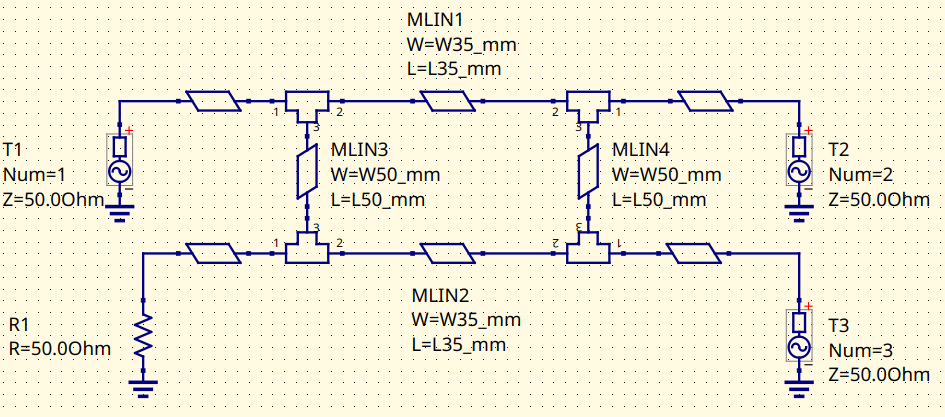
../../../_images/2_2_MLIN_with_Junctions_Schematic.png — Branch-Line with microstrip lines. Schematic

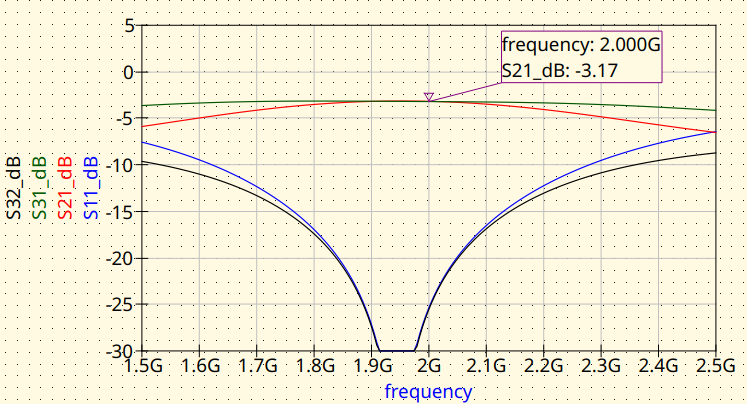
../../../_images/2_2_MLIN_with_Junctions_Magnitude.png — Branch-Line with microstrip lines. Magnitude response

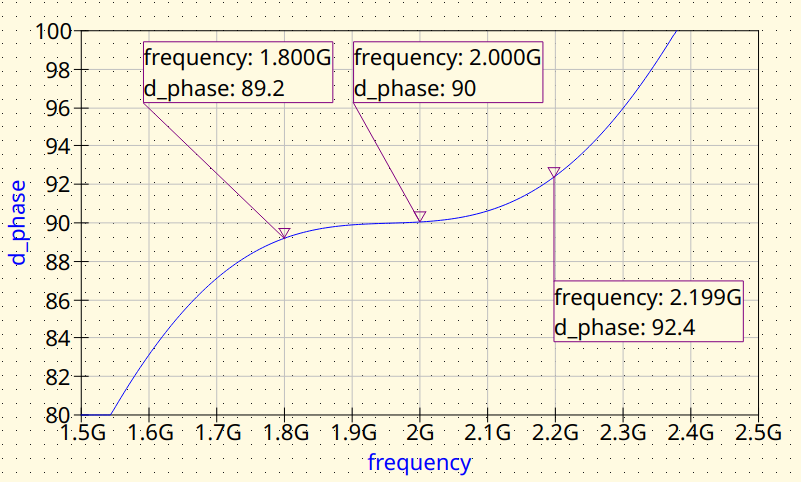
../../../_images/2_2_MLIN_with_Junctions_DPhase.png — Branch-Line with microstrip lines. Phase difference between outputs

2.3 MS: Fine Tuning

The loading of the junctions need to be corrected to have the Branch-Line coupler working at 2000 MHz. The circuit variables are tuned for this.

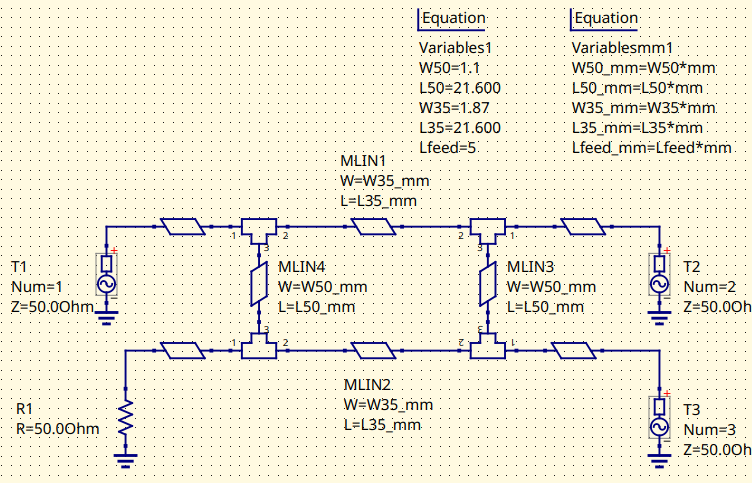
../../../_images/2_3_MLIN_FineTuned_Schematic.png — Fined-tuned Branch-Line coupler (MS). Schematic

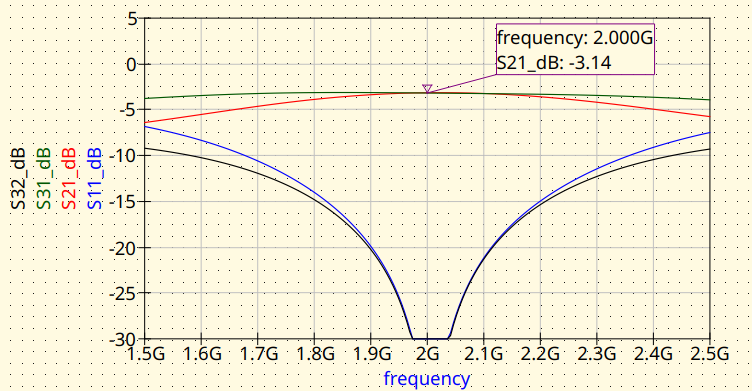
../../../_images/2_3_MLIN_FineTuned_Magnitude.png — Fined-tuned Branch-Line coupler (MS). Magnitude response

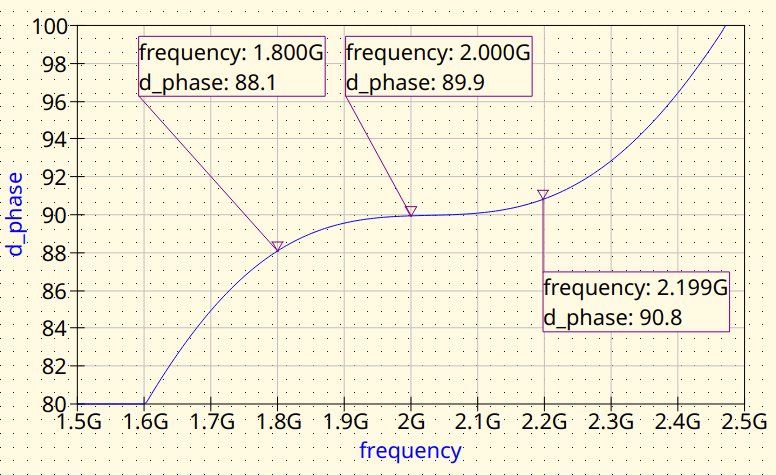
../../../_images/2_3_MLIN_FineTuned_DPhase.png — Fined-tuned Branch-Line coupler (MS). Phase difference between outputs

3. EM simulation

Once the microstrip model is good enough, then it’s convenient to validate it with an EM tool. EMerge software is particularly well suited for this. The reader is encourage to install EMerge from GitHub and give it a try.

The model definition is as follows:

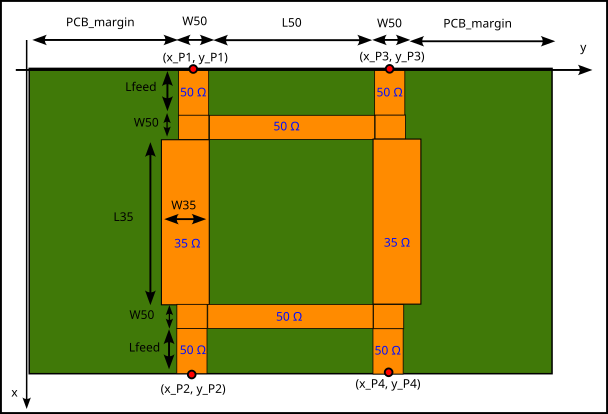
And this is the Python script for running the simulation:

import matplotlib
matplotlib.use('WebAgg')
import matplotlib.pyplot as plt
import subprocess # Used to run the post-processing script
import emerge as em
import numpy as np
import time
from datetime import datetime

# ---------------------------------------------------------------------------
# PROJECT NAME
# ---------------------------------------------------------------------------
project_name = "Branch-Line Coupler 2000 MHz"


# ---------------------------------------------------------------------------
# Unit definitions
# ---------------------------------------------------------------------------
mm  = 1e-3         # m
mil = 0.0254 * mm  # meter per mil
MHz = 1e6          # Hz

# ---------------------------------------------------------------------------
# Substrate / material
# ---------------------------------------------------------------------------
er  = 3.55         # RO4003C relative permittivity
th  = 0.508        # [mm] (20 mil) Substrate thickness
tand = 0.0029      # Substrate tand

# ---------------------------------------------------------------------------
# Center frequency
# ---------------------------------------------------------------------------
f0_MHz = 2000;
f0 = f0_MHz*MHz    # centre frequency (Hz)

# ---------------------------------------------------------------------------
# Branch-line circuit model parameters
# ---------------------------------------------------------------------------
W50  = 1.1         # [mm] Trace width for 50-Ohm arms
W35  = 1.87        # [mm] Trace width for 35-Ohm arms

L35  = 22          # [mm] Quarter-wave length, 35-Ohm shunt arms
L50  = 22          # [mm] Quarter-wave length, 75-Ohm series arms

L_feed = 5         # [mm] Feed-line length

# ---------------------------------------------------------------------------
# Simulation setup
# ---------------------------------------------------------------------------
model = em.Simulation(project_name)
model.check_version("2.3.0")

# ---------------------------------------------------------------------------
# Frequency sweep
# ---------------------------------------------------------------------------
f_start = 100*MHz
f_stop = 3000*MHz
n_points = 40

# ---------------------------------------------------------------------------
# Material and PCB layouter
# ---------------------------------------------------------------------------
mat = em.Material(er=er, tand=tand, color="#488343", opacity=0.4)
pcb = em.geo.PCBNew(th, unit=mm, material=mat)

# ---------------------------------------------------------------------------
# Layout
# ---------------------------------------------------------------------------
pcb_margin = 25 # Space at both sides of the copper traces

# Port 1
x_P1 = 0
y_P1 = pcb_margin+W50/2

# Input feed line
pcb.new(x_P1, y_P1, W50, (-1, 0)).straight(L_feed)['p1']  # P1: input

# Input feedline tee
pcb.new(x_P1, y_P1, W50, (1, 0)).straight(W50)

# Input-side 35 Ohm line
pcb.new(x_P1+W50, y_P1, W35, (1, 0)).straight(L35)

# In-phase output tee
pcb.new(x_P1+W50+L35, y_P1, W50, (1, 0)).straight(W50)

# In-phase output port position
x_P2 = x_P1+W50+L35+W50
y_P2 = y_P1

# In-phase output feed line
pcb.new(x_P2, y_P2, W50,  (1, 0)).straight(L_feed)['p2']   # P2: in-phase output


# Isolated port
x_P3 = 0
y_P3 = pcb_margin+W50+L50+W50/2

# Isolated port feed line
pcb.new(x_P3, y_P3, W50, (-1, 0)).straight(L_feed)['p3']  # P3: Isolated port

# Isolated port tee
pcb.new(x_P3, y_P3, W50, (1, 0)).straight(W50)

# Isolated port-side 35 Ohm line
pcb.new(x_P3+W50, y_P3, W35, (1, 0)).straight(L35)

# Quadrature-output-side tee
pcb.new(x_P3+W50+L35, y_P3, W50, (1, 0)).straight(W50)

# Quadrature-output-side feed line
pcb.new(x_P3+W50+L35+W50, y_P3, W50, (1, 0)).straight(L_feed)

# Quadrature output port position
x_P4 = x_P3+W50+L35+W50
y_P4 = y_P3

pcb.new(x_P4, y_P4, W50, (1, 0)).straight(L_feed)['p4']   # P4: quadrature output

# Input-side 50 Ohm line joining the 35 Ohm branchline_post
pcb.new(x_P1+W50/2, y_P1+W50/2, W50, (0,1)).straight(L50)

# Output-side 50 Ohm line joining the 35 Ohm branchline_post
pcb.new(x_P2-W50/2, y_P2+W50/2, W50, (0,1)).straight(L50)


coupler = pcb.compile_paths(merge=True)

# ---------------------------------------------------------------------------
# Bounding box, dielectric and air
# ---------------------------------------------------------------------------
pcb.determine_bounds(topmargin=pcb_margin, bottommargin=pcb_margin)
diel = pcb.generate_pcb()
air  = pcb.generate_air(4 * th)

# ---------------------------------------------------------------------------
# Modal ports
# ---------------------------------------------------------------------------
p1 = pcb.modal_port(pcb['p1'], width_multiplier=5, height=4 * th)
p2 = pcb.modal_port(pcb['p2'], width_multiplier=5, height=4 * th)
p3 = pcb.modal_port(pcb['p3'], width_multiplier=5, height=4 * th)
p4 = pcb.modal_port(pcb['p4'], width_multiplier=5, height=4 * th)

# ---------------------------------------------------------------------------
# Solver settings
# ---------------------------------------------------------------------------
model.mw.set_resolution(0.2)
model.mw.set_frequency_range(f_start, f_stop, n_points)

# ---------------------------------------------------------------------------
# Assemble geometry
# ---------------------------------------------------------------------------
model.commit_geometry()

# ---------------------------------------------------------------------------
# Mesh refinement
# ---------------------------------------------------------------------------
model.mesher.set_boundary_size(coupler, 0.5 * mm, growth_rate=10)
model.mesher.set_face_size(p1, 0.5 * mm)
model.mesher.set_face_size(p2, 0.5 * mm)
model.mesher.set_face_size(p3, 0.5 * mm)
model.mesher.set_face_size(p4, 0.5 * mm)

# ---------------------------------------------------------------------------
# Mesh generation and visualisation
# ---------------------------------------------------------------------------
model.generate_mesh()
#model.view(plot_mesh=True)
model.view(plot_mesh=False)
# ---------------------------------------------------------------------------
# Boundary conditions
# ---------------------------------------------------------------------------
port1 = model.mw.bc.ModalPort(p1, 1, modetype='TEM')
port2 = model.mw.bc.ModalPort(p2, 2, modetype='TEM')
port3 = model.mw.bc.ModalPort(p3, 3, modetype='TEM')
port4 = model.mw.bc.ModalPort(p4, 4, modetype='TEM')

# ---------------------------------------------------------------------------
# Run solver
# ---------------------------------------------------------------------------
start_time = time.time()
data = model.mw.run_sweep(parallel=True, n_workers=8, frequency_groups=8)
run_time = (time.time() - start_time) / 60
print(f"Simulation completed in {run_time:.2f} minutes")

# ---------------------------------------------------------------------------
# Extract S-parameters (raw solver points)
# ---------------------------------------------------------------------------
grid = data.scalar.grid
f    = grid.freq

S11 = grid.S(1, 1)
S21 = grid.S(2, 1)
S31 = grid.S(3, 1)
S41 = grid.S(4, 1)
S42 = grid.S(4, 2)

# ---------------------------------------------------------------------------
# Vector fitting — supersampled plot
# ---------------------------------------------------------------------------
n_supersamples = 2001
f_fit   = np.linspace(f_start, f_stop, n_supersamples)
f_MHz = f_fit / 1e6    #  Scale for displaying the graphs
S11_fit = grid.model_S(1, 1, f_fit)
S21_fit = grid.model_S(2, 1, f_fit)
S31_fit = grid.model_S(3, 1, f_fit)
S41_fit = grid.model_S(4, 1, f_fit)
S42_fit = grid.model_S(4, 2, f_fit)

phase_S21   = np.angle(S21_fit, deg=True) # in-phase output
phase_S41   = np.angle(S41_fit, deg=True) # quadrature output
phase_diff  = phase_S21 - phase_S41

# ---------------------------------------------------------------------------
# 3-D field visualisation at f0
# ---------------------------------------------------------------------------
field = data.field.find(freq=f0)

model.display.add_object(diel)
model.display.add_object(coupler)
model.display.add_portmode(port1, k0=field.k0)
model.display.add_portmode(port2, k0=field.k0)
model.display.add_portmode(port3, k0=field.k0)
model.display.add_portmode(port4, k0=field.k0)
model.display.add_field(
    field.cutplane(0.5 * mm, z=-0.5 * th * mil).scalar('Ez', 'real'),
    symmetrize=True,
)
model.display.show()

# ---------------------------------------------------------------------------
# Export Touchstone
# ---------------------------------------------------------------------------
comments = [
    f"--- {project_name} ---",
    "Substrate: RO4003C",
    f"h = {th} mm",
    f"W50 = {W50} mm, W35 = {W35} mm",
    f"L35 = {L35} mm, L50 = {L50} mm",
    f"L_feed = {L_feed} mm",
    f"Run time = {run_time:.2f} min",
]

timestamp = datetime.now().strftime("%Y-%m-%d_%H-%M-%S")
grid.export_touchstone(project_name + "_EMerge_" + timestamp, custom_comments=comments)

# Save raw arrays for post-processing
np.savez(
    project_name + "_data.npz",
    f=f_fit, S11=S11_fit, S21=S21_fit, S31=S31_fit, S41=S41_fit, S42=S42_fit,
    phase_diff=phase_diff,
)


subprocess.run(["python", "branchline_post.py"], check=True)

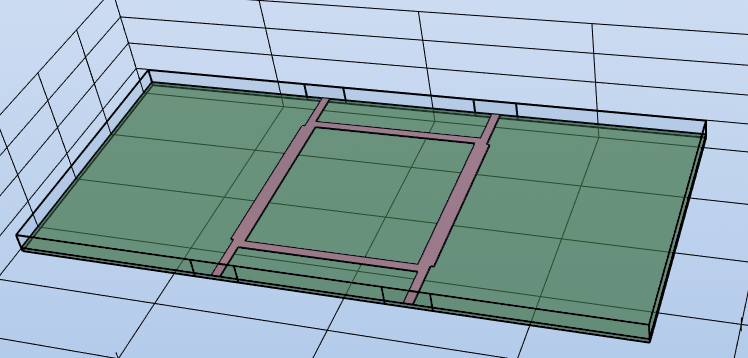
../../../_images/Branch-Line-3DView.png — EMerge 3D model view

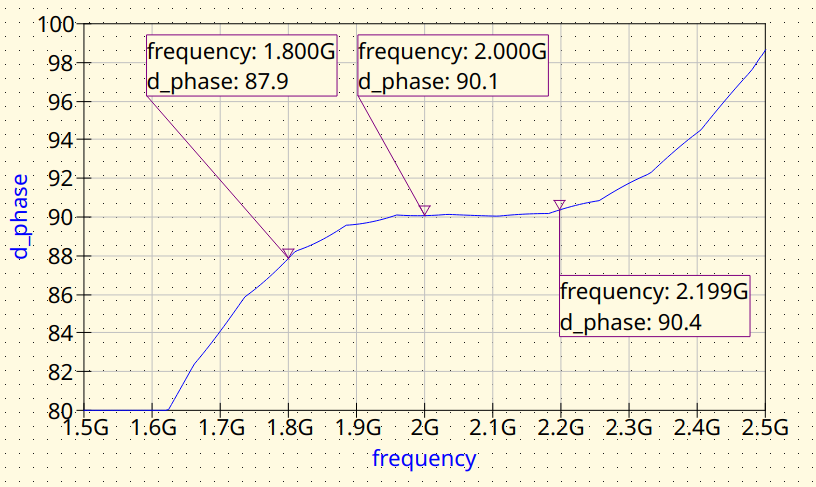
../../../_images/3_1_FirstApproach_Dphase.png — EMerge FEM simulation. Phase difference between outputs

3.1 Use design variables for 2.2

First, the system is modelled using the design variables obtained from step 2.2 as the input

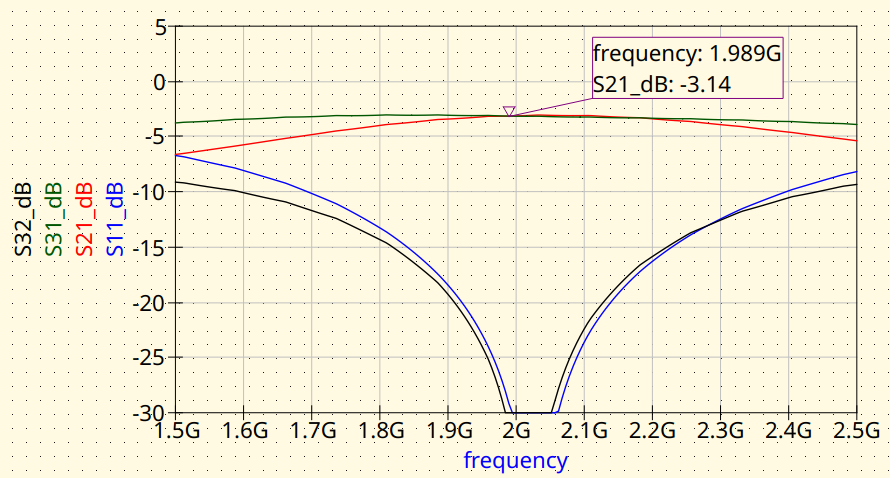
../../../_images/3_1_FirstApproach_Magnitude.png — EMerge FEM simulation. Magnitude response.

3.2 Fine-tuning

The reader may notice that the center frequency of the Branch-Line coupler is shifted towards high frequencies, so some retuning is needed.

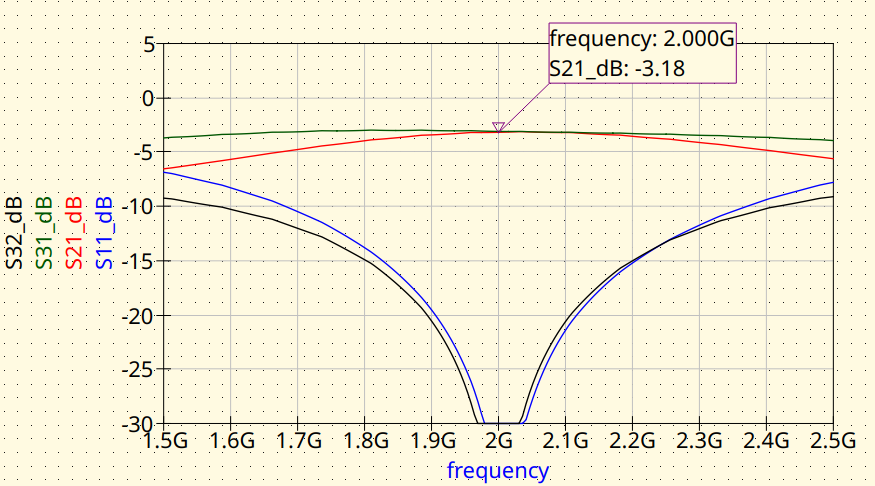
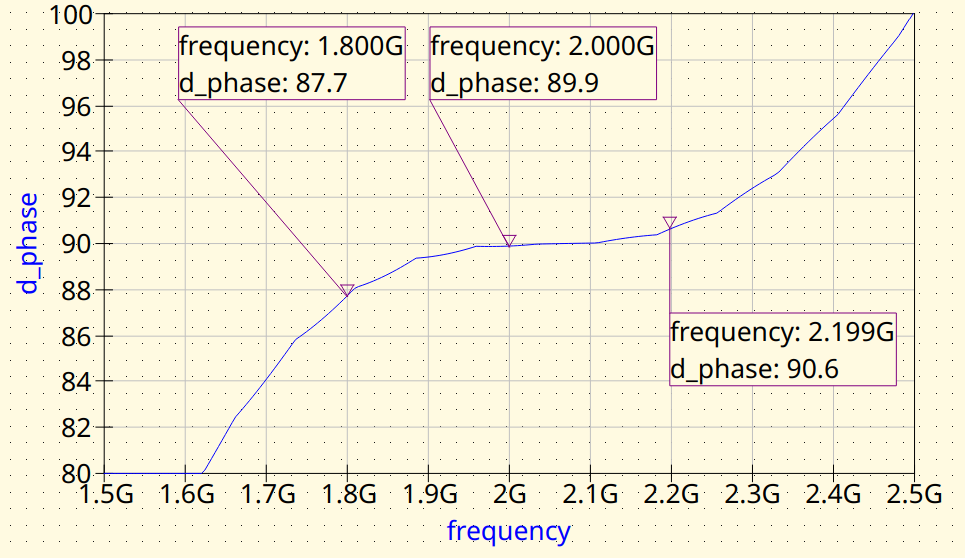
../../../_images/3_2_FineTuning_Dphase.png — EMerge FEM simulation. Phase difference between outputs